Recherche d'un cycle hamiltonien de longueur minimale
ou
Problème du voyageur de commerce
Introduction
Il s'agit d'implémenter et de comparer les résultats de trois ou quatre heuristiques (algorithme approché) qui déterminent sur un graphe non-orienté un cycle hamiltonien de valeur minimum. Un cycle hamiltonien est un cycle passant une fois et une seule par chaque sommet du graphe.
Le problème de la recherche d'un cycle hamiltonien de longueur minimale est à rapprocher de celui - classique - du voyageur de commerce. Si un voyageur de commerce, partant d'une ville de départ donnée, doit passer exactement une fois par chaque ville se trouvant sur sa liste puis revenir dans la ville initiale (chez lui), on peut comprendre qu'il ait intérêt à choisir l'ordre dans lequel il va choisir les villes, pour que la somme des distances qu'il aura à parcourir dans sa tournée soit aussi petite que possible. On considère qu'il connaît, pour chaque paire de villes, la distance les séparant. Ainsi, on peut penser qu'il a en sa possession toutes les données nécessaires pour trouver la tournée minimale, mais il n'est absolument pas évident de savoir comment utiliser ces données pour résoudre ce problème…
Celui-ci figure parmi les problèmes d'optimisation combinatoire classés difficiles. Il se rencontre dans de nombreuses situations comme par exemple des problèmes d'ordonnancement de production, de ramassage scolaire, de cablage de circuits, de synthèse des circuits logiques séquentiels… Il se modélise par la recherche d'un circuit hamiltonien (cas orienté) ou d'un cycle hamiltonien (cas non orienté) dans le graphe dont l'ensemble des sommets représente les différents sites et l'ensemble des arcs (ou des arêtes) les liaisons entre ces sites.
Il s'agit d'un problème NP-difficile, c'est-à-dire qu'il n'existe pas d'algorithme à complexité polynomiale pour le résoudre dans le cas général. Néanmoins, un certain nombre d'heuristiques (algorithmes approximatifs) ont été développées pour déterminer de "bonnes" solutions à des instances du problème. Par "bonne", on entend une solution qui, si elle n'est pas la solution optimale, n'en est pas "trop" éloignée.
Nous nous intéresserons plus particulièrement à des méthodes heuristiques simples de résolution, même si, en fait, il existe énormément d'algorithmes permettant de résoudre - plus ou moins efficacement - le problème du voyageur de commerce :
- Méthodes de descente
- Algorithmes gloutons
- Méthode Branch & Bound
- Recuit simulé
- Algorithme tabou
- Algorithmes génétiques
- Algorithme de Lin et Kerningham
- Colonies de fourmis
Nous allons donc pouvoir comparer sur différents exemples l'efficacité de des algorithmes nommés :
- Nearest Neighbour Algorithm (NNA)
- Nearest Addition Algorithm (NAA)
- Nearest Insertion Algorithm (NIA)
- Cheapest Insertion Algorithm (CIA)
- Farthest Insertion Algorithm (FIA)
Algorithmes des heuristiques retenues
- Nearest Neighbour Algorithm (NNA)
- On part d'une tournée réduite à un seul site vi1.
- Tant que tous les sites ne sont pas incorporés dans la tournée répéter
- Soit vi1,vi2,...,vik (k inférieur à n) la solution courante (chaîne) à l'itération k, on rajoute le site vik+1 le plus proche de vik à la fin de la chaîne.
- Fin répéter
- Nearest Addition Algorithm (NAA)
- T
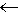 v0 /* on part d'une tournée réduite à un seul site v0 */
v0 /* on part d'une tournée réduite à un seul site v0 */
- Tant que tous les sites ne sont pas incorporés dans la tournée T répéter
- Soit vj
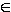 T et vk
T et vk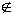 T tels que d(vj,vk) soit minimum
T tels que d(vj,vk) soit minimum
- Soit (vi,vj) une des deux arêtes extrémité de vj dans T
- T
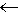 T\(vi,vj)
T\(vi,vj)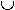 {(vi,vk),(vk,vj)}
{(vi,vk),(vk,vj)}
- Fin répéter
- Nearest Insertion Algorithm (NIA)
- T
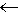 v0 /* on part d'une tournée réduite à un seul site v0 */
v0 /* on part d'une tournée réduite à un seul site v0 */
- Tant que tous les sites ne sont pas incorporés dans la tournée T répéter
- Soit vj
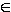 T et vk
T et vk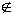 T tels que d(vj,vk) soit minimum
T tels que d(vj,vk) soit minimum
- Soit vi le point voisin de vj dans T tel que d(vi,vk)+d(vk,vj)-d(vi,vj) est minimum
- T
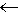 T\(vi,vj)
T\(vi,vj)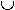 {(vi,vk),(vk,vj)}
{(vi,vk),(vk,vj)}
- Fin répéter
- Cheapest Insertion Algorithm (CIA)
- T
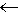 v0 /* on part d'une tournée réduite à un seul site v0 */
v0 /* on part d'une tournée réduite à un seul site v0 */
- Tant que tous les sites ne sont pas incorporés dans la tournée T répéter
- Soit vk
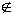 T et (vi,vj) une arête de T telle que d(vi,vk)+d(vk,vj)-d(vi,vj) est minimum
T et (vi,vj) une arête de T telle que d(vi,vk)+d(vk,vj)-d(vi,vj) est minimum
- T
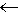 T\(vi,vj)
T\(vi,vj)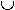 {(vi,vk),(vk,vj)}
{(vi,vk),(vk,vj)}
- Fin répéter
- Farthest Insertion Algorithm (FIA)
- T
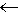 v0 /* on part d'une tournée réduite à un seul site v0 */
v0 /* on part d'une tournée réduite à un seul site v0 */
- Tant que tous les sites ne sont pas incorporés dans la tournée T répéter
- Soit vk
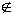 T tel que min{d(vj,vk) | vj
T tel que min{d(vj,vk) | vj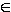 T} soit maximum
T} soit maximum
- Soit (vi,vj) une arête de T telle que d(vi,vk)+d(vk,vj)-d(vi,vj) est minimum
- T
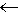 T\(vi,vj)
T\(vi,vj)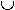 {(vi,vk),(vk,vj)}
{(vi,vk),(vk,vj)}
- Fin répéter
Applet Java illustrant toutes ces heuristiques
Conclusion : étude comparative des heuristiques
Nous pouvons maintenant comparer les résultats fournis par les cinq heuristiques. Pour cette comparaison, et dans un souci de clarté, portons sur un même graphique la longueur moyenne de la tournée, calculée sur 100 itérations pour chaque heuristique, en fonction du nombre de points.
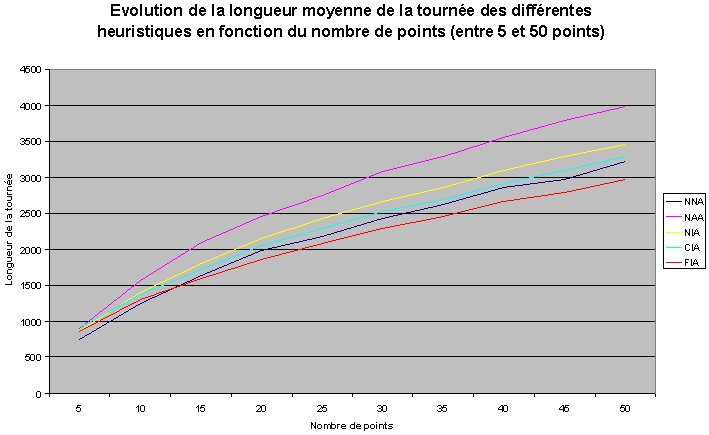
Pour un petit nombre de points, on peut constater que l'algorithme NNA, le plus simple qui soit (à chaque étape, on se dirige vers la ville la plus proche), donne de biens meilleurs résultats que les quatre autres. Puis, pour des cartes ayant entre 10 et 15 villes, la tendance s'inverse avec l'algorithme le plus élaboré, l'algorithme FIA, qui devient alors plus avantageux.
L'algorithme NAA, insérant dans la tournée aléatoirement le point qui en est le plus proche, est en revanche immédiatement beaucoup plus mauvais que les quatre autres.
On peut alors ce demander ce qu'il adviendra lorsque le nombre de points va augmenter.
Pour un nombre de points allant jusqu'à 200, on se rend compte que la tendance qui se révélait au bout de 50 points se confirme très nettement.
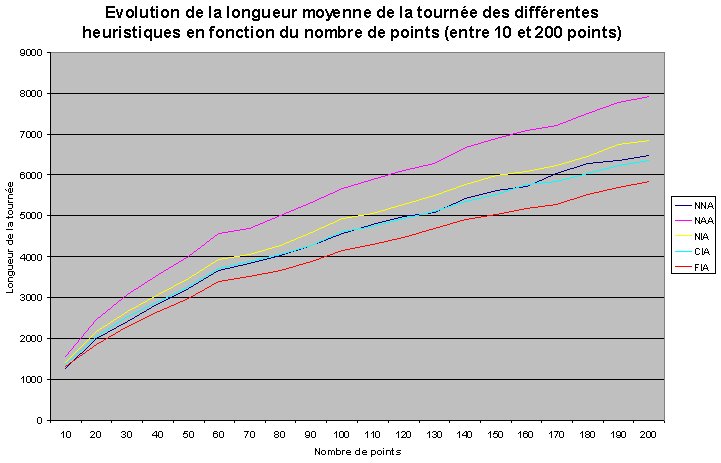
En effet, l'algorithme NAA donne des résultats de plus en plus mauvais, et finit en dernier de ces heuristiques, tandis que l'algorithme FIA confirme ses très bons résultats quand le nombre de points augmente.
De plus, l'algorithme "Nearest Neighbour" (NNA), qui se classait en second pour de petits nombres de points, passe en troisième quand le nombre de points augmente. Il paraît quand même étonnant que cet algorithme, très simple, parvienne à d'aussi bons résultats, par rapport à l'heuristique FIA.
Il semble en revanche normal que l'algorithme CIA se classe systématiquement devant l'algorithme NIA, car au lieu d'insérer au mieux l'élément le plus proche de la tournée, il cherche d'emblée le point qui s'insèrera le mieux dans la tournée. On peut aussi remarquer que NNA et CIA donnent des solutions assez proches en ce qui concerne la longueur de la tournée.
Ces méthodes ont le mérite de procurer rapidement une solution à un problème. Elles peuvent de plus être utilisées comme solution courante de départ dans un algorithme "Branch and Bound" ou dans des méthodes de voisinage.
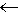 v0 /* on part d'une tournée réduite à un seul site v0 */
v0 /* on part d'une tournée réduite à un seul site v0 */
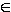 T et vk
T et vk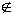 T tels que d(vj,vk) soit minimum
T tels que d(vj,vk) soit minimum
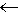 T\(vi,vj)
T\(vi,vj)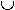 {(vi,vk),(vk,vj)}
{(vi,vk),(vk,vj)}
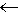 v0 /* on part d'une tournée réduite à un seul site v0 */
v0 /* on part d'une tournée réduite à un seul site v0 */
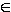 T et vk
T et vk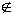 T tels que d(vj,vk) soit minimum
T tels que d(vj,vk) soit minimum
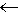 T\(vi,vj)
T\(vi,vj)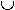 {(vi,vk),(vk,vj)}
{(vi,vk),(vk,vj)}
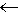 v0 /* on part d'une tournée réduite à un seul site v0 */
v0 /* on part d'une tournée réduite à un seul site v0 */
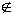 T et (vi,vj) une arête de T telle que d(vi,vk)+d(vk,vj)-d(vi,vj) est minimum
T et (vi,vj) une arête de T telle que d(vi,vk)+d(vk,vj)-d(vi,vj) est minimum
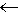 T\(vi,vj)
T\(vi,vj)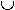 {(vi,vk),(vk,vj)}
{(vi,vk),(vk,vj)}
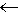 v0 /* on part d'une tournée réduite à un seul site v0 */
v0 /* on part d'une tournée réduite à un seul site v0 */
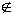 T tel que min{d(vj,vk) | vj
T tel que min{d(vj,vk) | vj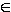 T} soit maximum
T} soit maximum
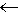 T\(vi,vj)
T\(vi,vj)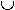 {(vi,vk),(vk,vj)}
{(vi,vk),(vk,vj)}

